Category Archives: Science and Religion

The Dynamic Quality of Henri Bergson

Posted on by

Robert Pirsig writes in Lila that Quality contains a dynamic good in addition to a static good. This dynamic good consists of a search for “betterness” that is unplanned and has no specific destination, but is nevertheless responsible for all progress. Once a dynamic good solidifies into a concept, practice, or tradition in a culture, it becomes a static good. Creativity, mysticism, dreams, and even good guesses or luck are examples of dynamic good in action. Religious traditions, laws, and science textbooks are examples of static goods.

Pirsig describes dynamic quality as the “pre-intellectual cutting edge of reality.” By this, he means that before concepts, logic, laws, and mathematical formulas are discovered, there is process of searching and grasping that has not yet settled into a pattern or solution. For example, invention and discovery is often not an outcome of calculation or logical deduction, but of a “free association of ideas” that tends to occur when one is not mentally concentrating at all. Many creative people, from writers to mathematicians, have noted that they came up with their best ideas while resting, engaging in everyday activities, or dreaming.

Dynamic quality is not just responsible for human creation — it is fundamental to all evolution, from the physical level of atoms and molecules, to the biological level of life forms, to the social level of human civilization, to the intellectual level of human thought. Dynamic quality exists everywhere, but it has no specific goals or plans — it always consists of spur-of-the-moment actions, decisions, and guesses about how to overcome obstacles to “betterness.”

It is difficult to conceive of dynamic quality — by its very nature, it is resistant to conceptualization and definition, because it has no stable form or structure. If it did have a stable form or structure, it would not be dynamic.

However the French philosopher Henri Bergson (1859-1941) provided a way to think about dynamic quality, by positing change as the fundamental nature of reality. (See Beyond the “Mechanism” Metaphor in Physics.) In Bergson’s view, traditional reason, science, and philosophy created static, eternal forms and posited these forms as the foundation of reality — but in fact these forms were tools for understanding reality and not reality itself. Reality always flowed and was impossible to fully capture in any static conceptual form. This flow could best be understood through perception rather than conception. Unfortunately, as philosophy created larger and larger conceptual categories, philosophy tended to become dominated by empty abstractions such as “substance,” “numbers,” and “ideas.” Bergson proposed that only an intuitive approach that enlarged perceptual knowledge through feeling and imagination could advance philosophy out of the dead end of static abstractions.

________________________

The Flow of Time

Bergson argued that we miss the flow of time when we use the traditional tools of science, mathematics, and philosophy. Science conceives of time as simply one coordinate in a deterministic space-time block ruled by eternal laws; mathematics conceives of time as consisting of equal segments on a graph; and philosophers since Plato have conceptualized the world as consisting of the passing shadows of eternal forms.

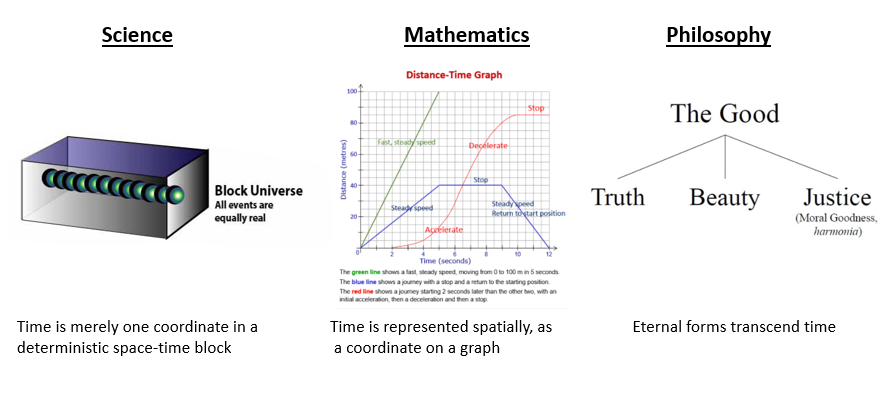
These may be useful conceptualizations, argues Bergson, but they do not truly grasp time. Whether it is an eternal law, a graph, or an eternal form, such depictions are snapshots of reality; they do not and cannot represent the indivisible flow of time that we experience. The laws of science in particular neglected the elements of indeterminism and freedom in the universe. (Henri Bergson once debated Einstein on this topic). The neglect of real change by science was the result of science’s ambition to foresee all things, which motivated scientists to focus on the repeatable and calculable elements of nature, rather than the genuinely new. (The Creative Mind, Mineola, New York: Dover, 2007, p. 3) Those events that could not be predicted were tossed aside as being merely random or unknowable. As for philosophy, Bergson complained that the eternal forms of the philosophers were empty abstractions — the categories of beauty and justice and truth were insufficient to serve as representations of real experience.

Actual reality, according to Bergson, consisted of “unceasing creation, the uninterrupted upsurge of novelty.” (The Creative Mind, p. 7) Time was not merely a coordinate for recording motion in a determinist universe; time was “a vehicle of creation and choice.” (p. 75) The reality of change could not be captured in static concepts, but could only be grasped intuitively. While scientists saw evolution as a combination of mechanism and random change, Bergson saw evolution as a result of a vital impulse (élan vital) that pervaded the universe. Although this vital impetus possessed an original unity, individual life forms used this vital impetus for their own ends, creating conflict between life forms. (Creative Evolution, pp. 50-51)

Biologists attacked Bergson on the grounds that there was no “vital impulse” that they could detect and measure. But biologists argued from the reductionist premise that everything could be explained by reference to smaller parts, and since there was no single detectable force animating life, there was no “vital impetus.” But Bergson’s premise was holistic, referring to the broader action of organic development from lower orders to higher orders, culminating in human beings. There was no separate force — rather entities organized, survived, and reproduced by absorbing and processing energy, in multiple forms. In the words of one eminent biologist, organisms are “resilient patterns . . . in an energy flow.” There is no separate or unique energy of life – just energy.

The Superiority of Perception over Conception

Bergson believed with William James that all knowledge originated in perception and feeling; as human mental powers increased, conceptual categories were created to organize and generalize what we (and others) discovered through our senses. Concepts were necessary to advance human knowledge, of course. But over time, abstract concepts came to dominate human thought to the point at which pure ideas were conceived as the ultimate reality — hence Platonism in philosophy, mathematical Platonism in mathematics, and eternal laws in science. Bergson believed that although we needed concepts, we also needed to rediscover the roots of concepts in perception and feeling:

If the senses and the consciousness had an unlimited scope, if in the double direction of matter and mind the faculty of perceiving was indefinite, one would not need to conceive any more than to reason. Conceiving is a make-shift when perception is not granted to us, and reasoning is done in order to fill up the gaps of perception or to extend its scope. I do not deny the utility of abstract and general ideas, — any more than I question the value of bank-notes. But just as the note is only a promise of gold, so a conception has value only through the eventual perceptions it represents. . . . the most ingeniously assembled conceptions and the most learnedly constructed reasonings collapse like a house of cards the moment the fact — a single fact rarely seen — collides with these conceptions and these reasonings. There is not a single metaphysician, moreover, not one theologian, who is not ready to affirm that a perfect being is one who knows all things intuitively without having to go through reasoning, abstraction and generalisation. (The Creative Mind, pp. 108-9)

In the end, despite their obvious utility, the conceptions of philosophy and science tend “to weaken our concrete vision of the universe.” (p. 111) But we clearly do not have God-like powers to perceive everything, and we are not likely to get such powers. So what do we do? Bergson argues that instead of “trying to rise above our perception of things” through concepts, we “plunge into [perception] for the purpose of deepening it and widening it.” (p. 111) But how exactly are we to do this?

Enlarging Perception

There is one group of people, argues Bergson, that have mastered the ability to deepen and widen perception: artists. From paintings to poetry to novels and musical compositions, artists are able to show us things and events that we do not directly perceive and evoke a mood within us that we can understand even if the particular form that the artist presents may never have been seen or heard by us before. Bergson writes that artists are idealists who are often absent-mindedly detached from “reality.” But it is precisely because artists are detached from everyday living that they are able to see things that ordinary, practical people do not:

[Our] perception . . . isolates that part of reality as a whole that interests us; it shows us less the things themselves than the use we can make of them. It classifies, it labels them beforehand; we scarcely look at the object, it is enough for us to know which category it belongs to. But now and then, by a lucky accident, men arise whose senses or whose consciousness are less adherent to life. Nature has forgotten to attach their faculty of perceiving to their faculty of acting. When they look at a thing, they see it for itself, and not for themselves. They do not perceive simply with a view to action; they perceive in order to perceive — for nothing, for the pleasure of doing so. In regard to a certain aspect of their nature, whether it be their consciousness or one of their senses, they are born detached; and according to whether this detachment is that of a particular sense, or of consciousness, they are painters or sculptors, musicians or poets. It is therefore a much more direct vision of reality that we find in the different arts; and it is because the artist is less intent on utilizing his perception that he perceives a greater number of things. (The Creative Mind, p. 114)

The Method of Intuition

Bergson argued that the indivisible flow of time and the holistic nature of reality required an intuitive approach, that is “the sympathy by which one is transported into the interior of an object in order to coincide with what there is unique and consequently inexpressible in it.” (The Creative Mind, p. 135) Analysis, as in the scientific disciplines, breaks down objects into elements, but this method of understanding is a translation, an insight that is less direct and holistic than intuition. The intuition comes first, and one can pass from intuition to analysis but not from analysis to intuition.

In his essay on the French philosopher Ravaisson, Bergson underscored the benefits and necessity of an intuitive approach:

[Ravaisson] distinguished two different ways of philosophizing. The first proceeds by analysis; it resolves things into their inert elements; from simplification to simplification it passes to what is most abstract and empty. Furthermore, it matters little whether this work of abstraction is effected by a physicist that we may call a mechanist or by a logician who professes to be an idealist: in either case it is materialism. The other method not only takes into account the elements but their order, their mutual agreement and their common direction. It no longer explains the living by the dead, but, seeing life everywhere, it defines the most elementary forms by their aspiration toward a higher form of life. It no longer brings the higher down to the lower, but on the contrary, the lower to the higher. It is, in the real sense of the word, spiritualism. (p. 202)

From Philosophy to Religion

A religious tendency is apparent in Bergson’s philosophical writings, and this tendency grew more pronounced as Bergson grew older. It is likely that Bergson saw religion as a form of perceptual knowledge of the Good, widened by imagination. Bergson’s final major work, The Two Sources of Morality and Religion (Notre Dame, IN: University of Notre Dame Press, 1977) was both a philosophical critique of religion and a religious critique of philosophy, while acknowledging the contributions of both forms of knowledge. Bergson drew a distinction between “static religion,” which he believed originated in social obligations to society, and “dynamic religion,” which he argued originated in mysticism and put humans “in the stream of the creative impetus.” (The Two Sources of Morality and Religion, p. 179)

Bergson was a harsh critic of the superstitions of “static religion,” which he called a “farrago of error and folly.” These superstitions were common in all cultures, and originated in human imagination, which created myths to explain natural events and human history. However, Bergson noted, static religion did play a role in unifying primitive societies and creating a common culture within which individuals would subordinate their interests to the common good of society. Static religion created and enforced social obligations, without which societies could not endure. Religion also provided comfort against the depressing reality of death. (The Two Source of Morality and Religion, pp. 102-22)

In addition, it would be a mistake, Bergson argued, to suppose that one could obtain dynamic religion without the foundation of static religion. Even the superstitions of static religion originated in the human perception of a beneficent virtue that became elaborated into myths. Perhaps thinking that a cool running spring or a warm fire on the hearth as the actions of spirits or gods were a case of imagination run rampant, but these were still real goods, as were the other goods provided by the pagan gods.

Dynamic religion originated in static religion, but also moved above and beyond it, with a small number of exceptional human beings who were able to reach the divine source: “In our eyes, the ultimate end of mysticism is the establishment of a contact . . . with the creative effort which life itself manifests. This effort is of God, if it is not God himself. The great mystic is to be conceived as an individual being, capable of transcending the limitations imposed on the species by its material nature, thus continuing and extending the divine action.” (pp. 220-21)

In Bergson’s view, mysticism is intuition turned inward, to the “roots of our being , and thus to the very principle of life in general.” (p. 250) Rational philosophy cannot fully capture the nature of mysticism, because the insights of mysticism cannot be captured in words or symbols, except perhaps in the word “love”:

God is love, and the object of love: herein lies the whole contribution of mysticism. About this twofold love the mystic will never have done talking. His description is interminable, because what he wants to describe is ineffable. But what he does state clearly is that divine love is not a thing of God: it is God Himself. (p. 252)

Even so, just as the dynamic religion bases its advanced moral insights in part on the social obligations of static religion, dynamic religion also must be propagated through the images and symbols supplied by the myths of static religion. (One can see this interplay of static and dynamic religion in Jesus and Gandhi, both of whom were rooted in their traditional religions, but offered original teachings and insights that went beyond their traditions.)

Toward the end of his life, Henri Bergson strongly considered converting to Catholicism (although the Church had already placed three of Bergson’s works on its Index of Prohibited Books). Bergson saw Catholicism as best representing his philosophical inclinations for knowing through perception and intuition, and for joining the vital impetus responsible for creation. However, Bergson was Jewish, and the anti-Semitism of 1930s and 1940s Europe made him reluctant to officially break with the Jewish people. When the Nazis conquered France in 1940 and the Vichy puppet government of France decided to persecute Jews, Bergson registered with the authorities as a Jew and accepted the persecutions of the Vichy regime with stoicism. Bergson died in 1941 at the age of 81.

Once among the most celebrated intellectuals in the world, today Bergson is largely forgotten. Even among French philosophers, Bergson is much less known than Descartes, Sartre, Comte, and Foucault. It is widely believed that Bergson lost his debate with Einstein in 1922 on the nature of time. (See Jimena Canales, The Physicist and the Philosopher: Einstein, Bergson, and the Debate that Changed Our Understanding of Time, p. 6) But it is recognized today even among physicists that while Einstein’s conception of spacetime in relativity theory is an excellent theory for predicting the motion of objects, it does not disprove the existence of time and real change. It is also true that Bergson’s writings are extraordinarily difficult to understand at times. One can go through pages of dense, complex text trying to understand what Bergson is saying, get suddenly hit with a colorful metaphor that seems to explain everything — and then have a dozen more questions about the meaning of the metaphor. Nevertheless, Bergson remains one of the very few philosophers who looked beyond eternal forms to the reality of a dynamic universe, a universe moved by a vital impetus always creating, always changing, never resting.

Are Human Beings Just Atoms?

Posted on by

In a previous essay on materialism, I discussed the bizarre nature of phenomena on the subatomic level, in which particles have no definite position in space until they are observed. Referencing the works of several physicists and philosophers, I put forth the view that reality consists not of tiny, solid objects but rather bundles of properties and qualities that emerge from potentiality to actuality. In this view, when one breaks down reality into smaller and smaller parts, one does not reach the fundamental units of matter; rather, one is gradually unbundling properties and qualities until the smallest objects no longer even have a definite position in space!

Why is this important? One reason is that the enormous prestige and accomplishments of science have sometimes led us down the wrong path in properly describing and interpreting reality. Science excels at advancing our knowledge of how things work, by breaking down wholes into component parts and manipulating those parts into better arrangements that benefit humanity. This is how we got modern medicine, computers, air conditioning, automobiles, and space travel. However, science sometimes falls short in properly describing and interpreting reality, precisely because it focuses more on the parts than the wholes.

This defect in science becomes particularly glaring when certain scientists attempt to describe what human beings are like. All too often there is a tendency to reduce humans to their component parts, whether these parts are chemical elements (atoms), chemical compounds (molecules), or the much larger molecules known as genes. However, while these component parts make up human beings, there are properties and qualities in human beings that cannot be adequately described in terms of these parts.

Marcelo Gleiser, a physicist at Dartmouth College, argues that “life is the property of a complex network of biochemical reactions . . . a kind of hungry chemistry that is able to duplicate itself.” Biologist Richard Dawkins claims that humans are “just gene machines,” and “living organisms and their bodies are best seen as machines programmed by the genes to propagate those very same genes,” though he qualifies his statement by noting that “there is a very great deal of complication, and indeed beauty in being a gene machine.” Philosopher Daniel Dennett claims that human beings are “moist robots” and the human mind is a collection of computer-like information processes which happen to take place in carbon-based rather than silicon-based hardware.

Now it is true that human beings are composed of atoms that are the basis of chemicals and molecules, that are the basis of chemical compounds, such as genes. The issue, however, is whether describing the parts that compose a human being is the same as describing the whole human being. Yes, human beings are composed of atoms of oxygen, carbon, hydrogen, nitrogen, calcium, and phosphorous. But these atoms can be found in many, many places throughout the universe, in varying quantities and combinations, and they do not have human qualities unless and until they are organized in just the right way. Likewise, genes are ubiquitous in life forms ranging from mammals to lizards to plants to bacteria. Even viruses have genes, though most scientists argue that viruses are not true life forms because they need a host to reproduce. Nevertheless, while human beings share a very few properties and qualities with bacteria and viruses, humans clearly have many properties and qualities that the lower life forms do not.

In fact, recognizing the very difference between life and death can be lost by excessive focus on atoms and molecules. Consider the following: an emergency room doctor treats a patient suffering from a heart attack. Despite the physician’s best efforts, despite all of the doctor’s training and knowledge, the patient dies on the table. So what is the difference between the patient that has died and the patient as he was several hours ago? The quantity and types of atoms composing the body are approximately the same as when the patient was alive. So what has changed? Obviously, the properties and qualities expressed by the organization of the atoms in the human being has changed. The heart no longer supplies blood to the rest of the body, the lungs no longer supply oxygen, the brain no longer has electrical activity, the human being no longer has the ability to run or walk or jump or talk or think or love. Atoms have to be organized in an extremely precise manner in order for these properties and qualities to emerge, and this organization has been lost. So if we are really going to accurately describe what a human being is, we have to refer not just to the atoms, but to the overall organization or form.

The issue of form is what separates the ancient Greek philosophers Democritus and Plato. Both philosophers believed that the universe and everything in it was composed of atoms; but Democritus thought that nothing existed but atoms and the void (space), whereas Plato believed that atoms were arranged by a creator, who, being essentially good, used ideal forms as a blueprint. Contrary to the views of Judaism, Christianity, and Islam, however, Plato believed that the creator was not omnipotent, and was forced to work with imperfect matter to do the best job possible, which is why most created objects and life forms were imperfect and fell short of the ideal forms.

Democritus would no doubt dismiss Plato’s ideal forms as being unreal — after all, forms are not something solid, so how can anything that is not solid, not made of material, exist at all? But as I’ve pointed out, the atoms that compose the human body are found everywhere, whereas actual, living human beings have these same atoms organized in a precise, particular form. In other words, in order to understand anything, it is not enough to break it down into parts and study the parts; one has to look at the whole. The properties and qualities of a living human being, as a whole, definitely do exist, or we would not know how to distinguish a living human being from a dead human being or any other existing thing composed of the same atoms.

The debate between Democritus and Plato points to a difference in ways of knowing that persist to this day: analytic knowledge and holistic knowledge. Analytic knowledge is pursued by science and reason; holistic knowledge is pursued by religion, art, and the humanities. The prestige of science and its technological accomplishments has elevated analytic understanding above all other forms of knowledge, but we remain lost without holistic understanding.

What precisely is “analytic knowledge”? The word “analyze” means “to study or determine the nature and relationship of the parts (of something) by analysis.” Synonyms for “analyze” include “break down,” “cut,” “deconstruct,” and “dissect.” In fact, the word “analysis” is derived from the New Latin word analyein, meaning “to break up.” Analysis is an extremely valuable tool and is responsible for human progress in all sorts of areas. But the knowledge derived from analysis is primarily a description and guide to how things work. It reduces knowledge of the whole to knowledge of the parts, which is fine if you want to take something apart and put it back together. But the knowledge of how things work is not the same as the knowledge of what things are as a whole, what qualities and properties they have, and the value of those qualities and properties. This latter knowledge is holistic knowledge.

The word “holism,” based on the ancient Greek word for “whole” (holos), was coined in the early twentieth century in order to promote the view that all systems, living or not, should be viewed as wholes and not just as a collection of parts or the sum of parts. It’s no accident that the words “whole,” “heal,” healthy,” and “holy” are linguistically related. The problems of sickness, malnutrition, and injury were well-known to the ancients, and it was natural for them to see these problems as a disturbance to the whole human being, rendering a person incomplete and missing certain vital functions. Wholeness was an ideal end, which made wholeness sacred (holy) as well. (For an extended discussion of analytic/reductionist knowledge vs. holistic knowledge, see this post.)

Holistic knowledge is not just about ideal physical health. It’s about ideal forms in all aspects, including the qualities we associate with human beings we admire: wisdom, strength, beauty, courage, love, kindness. As mistaken as religions have been in understanding natural causation, it is the devotion to ideal forms that is really the essence of religion. The ancient Greeks worshipped excellence, as embodied in their gods; Confucians were devoted to family ties and duties; the Jews submitted themselves to the laws of the one God; Christians devoted themselves to the love of God, embodied in Christ.

Holistic knowledge provides no guidance as to how to conduct surgery or build a computer or launch a rocket; but it does provide insight into the ethics of medicine, the desirability or hazards of certain types of technology, and the proper ends of human beings. All too often, contemporary secular societies expect new technologies to improve human lives and pay no heed to ideal human forms, on the assumption that ideal forms are a fantasy. Then we are shocked when the new technologies are abused and not only bring out the worst in human nature but enhance the power of the worst.

How Random is Evolution?

Posted on by

“Man is the product of causes which had no prevision of the end they were achieving . . . his origin, his growth, his hopes and fears, his loves and his beliefs, are but the outcome of accidental collocations of atoms. . . .” – Bertrand Russell

In high school or college, you were probably taught that human life evolved from lower life forms, and that evolution was a process in which random mutations in DNA, the genetic code, led to the development of new life forms. Most mutations are harmful to an organism, but some mutations confer an advantage to an organism, and that organism is able to flourish and pass down its genes to subsequent generations –hence, “survival of the fittest.”

Many people reject the theory of evolution because it seemingly removes the role of God in the creation of life and of human beings and suggests that the universe is highly disordered. But all available evidence suggests that life did evolve, that the world and all of its life was not created in six days, as the Bible asserted. Does this mean that human life is an accident, that there is no larger intelligence or purpose to the universe?

I will argue that although evolution does indeed suggest that the traditional Biblical view of life’s origins are incorrect, people have the wrong impression of (1) what randomness in evolution means and (2) how large the role of randomness is in evolution. While it is true that individual micro-events in evolution can be random, these events are part of a larger system, and this system can be highly ordered even if particular micro-events are random. Moreover, recent research in evolution indicates that in addition to random mutation, organisms can respond to environmental factors by changing in a manner that is purposive, not random, in a direction that increases their ability to thrive.

____________________

So what does it mean to say that something is “random”? According to the Merriam-Webster dictionary, “random” means “a haphazard course,” “lacking a definite plan, purpose, or pattern.” Synonyms for “random” include the words “aimless,” “arbitrary,” and “slapdash.” It is easy to see why when people are told that evolutionary change is a random process, that many reject the idea outright. This is not necessarily a matter of unthinking religious prejudice. Anyone who has examined nature and the biology of animals and human beings can’t help but be impressed by how enormously complex and precisely ordered these systems are. The fact of the matter is that it is extraordinarily difficult to build and maintain life; death and nonexistence is relatively easy. But what does it mean to lack “a definite plan, purpose, or pattern”? I contend that this definition, insofar as it applies to evolution, only refers to the particular micro-events of evolution when considered in isolation and not the broader outcome or the sum of the events.

Let me illustrate what I mean by presenting an ordinary and well-known case of randomness: rolling a single die. A die is a cube with six sides and a number, 1-6, on each side. The outcome of any roll of the die is random and unpredictable; if you roll a die once, the outcome will be unpredictable. If you roll a die multiple times, each outcome, as well as the particular sequence of outcomes, will be unpredictable. But if you look at the broader, long-term outcome after 1000 rolls, you will see this pattern: an approximately equal number of ones, twos, threes, fours, fives, and sixes will come up, and the average value of all events will be 3.5.

Why is this? Because the die itself is a highly-precise ordered system. Each die must have equally sided lengths on all sides and an equal distribution of density/weight throughout in order to make the outcome truly unpredictable, otherwise a gambler who knows the design of the die may have an edge. One die manufacturer brags, “With tolerances less than one-third the thickness of a human hair, nothing is left to chance.” [!] In fact, a common method of cheating with dice is to shave one or more sides or insert a weight into one end of the die. This results in a system that is also precisely ordered, but in a way that makes certain outcomes more likely. After a thousand rolls of the die, one or more outcomes will come up more frequently, and this pattern will stand out suspiciously. But the person who cheated by tilting the odds in one direction may have already escaped with his or her winnings.

If you look at how casinos make money, it is precisely by structuring the rules of each game to give the edge to the casino that allows them to make a profit in the long run. The precise outcome of each particular game is not known with certainty, the particular sequence of outcomes is not known, and the balance sheet of the casino at the end of the night cannot be predicted. But there is definitely a pattern: in the long run, the sum of events results in the casino winning and making a profit, while the players as a group will lose money. When casinos go out of business, it is generally because they can’t attract enough customers, not because they lose too many games.

The ability to calculate the sum of a sequence of random events is the basis of the so-called “Monte Carlo” method in mathematics. Basically, the Monte Carlo method involves setting certain parameters, selecting random inputs until the number of inputs is quite large, and then calculating the final result. It’s like throwing darts at a dartboard repeatedly and examining the pattern of holes. One can use this method with 30,000 randomly plotted points to calculate the value of pi to within 0.07 percent.

So if randomness can exist within a highly precise order, what is the larger order within which the random mutations of evolution operate? One aspect of this order is the bonding preferences of atoms, which are responsible not only for shaping how organisms arise, but how organisms eventually develop into astonishingly complex and wondrous forms. Without atomic bonds, structures would fall apart as quickly as they came together, preventing any evolutionary advances. The bonding preferences of atoms shape the parameters of development and result in molecular structures (DNA, RNA, and proteins) that retain a memory or blueprint, so that evolutionary change is incremental. The incremental development of organisms allows for the growth of biological forms that are eventually capable of running at great speeds, flying long distances, swimming underwater, forming societies, using tools, and, in the case of humans, building technical devices of enormous sophistication.

The fact of incremental change that builds upon previous advances is a feature of evolution that makes it more than a random process. This is illustrated by biologist Richard Dawkins’ “weasel program,” a computer simulation of how evolution works by combining random micro-events with the retaining of previous structures so that over time a highly sophisticated order can develop. The weasel program is based on the “infinite monkey theorem,” the fanciful proposal that an infinite number of monkeys with an infinite number of typewriters would eventually produce the works of Shakespeare. This theorem has been used to illustrate how order could conceivably emerge from random and mindless processes. What Dawkins did, however, was write a computer program to write just one sentence from Shakespeare’s Hamlet: “Methinks it is like a weasel.” Dawkins structured the computer program to begin with a single random sentence, reproduce this sentence repeatedly, but add random errors (“mutations”) in each “generation.” If the new sentence was at least somewhat closer to the target phrase “Methinks it is like a weasel,” that sentence became the new parent sentence. In this way, subsequent generations would gradually assume the form of the correct sentence. For example:

Generation 01: WDLTMNLT DTJBKWIRZREZLMQCO P
Generation 02: WDLTMNLT DTJBSWIRZREZLMQCO P
Generation 10: MDLDMNLS ITJISWHRZREZ MECS P
Generation 20: MELDINLS IT ISWPRKE Z WECSEL
Generation 30: METHINGS IT ISWLIKE B WECSEL
Generation 40: METHINKS IT IS LIKE I WEASEL
Generation 43: METHINKS IT IS LIKE A WEASEL

The Weasel program is a great example of how random change can produce order over time, BUT only under highly structured conditions, with a defined goal and a retaining of those steps toward that goal. Without these conditions, a computer program randomly selecting letters would be unlikely to produce the phrase “Methinks it is like a weasel” in the lifetime of the universe, according to Dawkins!

It is the retaining of most evolutionary advances, while allowing a small degree of randomness, that allows evolution to produce increasingly complex life forms. Reproduction has some random elements in it, but is actually remarkably precise and effective in producing offspring at least roughly similar to their parents. It is not the case that a female human is equally as likely to give birth to a dog, a pig, or a chicken as to give birth to a human. It would be very strange indeed if evolution was that random!

But there is even more to the story of evolution.

Recent research in biology has indicated that there are factors in nature that tend to push development in certain directions favorable to an organism’s flourishing. Even if you imagine evolution in nature as a huge casino, with a lot of random events, scientists have discovered that the players are strategizing: they are increasing or decreasing their level of gambling in response to environmental conditions, shaving the dice to obtain more favorable outcomes, and cooperating with each other to cheat the casino!

For example, it is now recognized among biologists that a number of microorganisms are capable to some extent of controlling their rate of mutation, increasing the rate of mutation during times of environmental challenge and stress, and suppressing the rate of mutation during times of peace and abundance. As a result of accelerated mutations, certain bacteria can acquire the ability to utilize new sources of nutrition, overcoming the threat of extinction arising from the depletion of its original food source. In other words, in response to feedback from the environment, organisms can decide to try to preserve as much of their genome as they can or experiment wildly in the hope of finding a solution to new environmental challenges.

The organism known as the octopus (a cephalopod) has a different strategy: it actively suppresses mutation in DNA and prefers to recode its RNA in response to environmental challenges. For example, octopi in the icy waters of the Antarctic recode their RNA in order to keep their nerves firing in cold water. This response is not random but directly adaptive. RNA recoding in octopi and other cephalopods is particularly prevalent in proteins responsible for the nervous system, and it is believed by scientists that this may explain why octopi are among the most intelligent creatures on Earth.

The cephalopods are somewhat unusual creatures, but there is evidence that other organisms can also adapt in a nonrandom fashion to their environment by employing molecular factors that suppress or activate the expression of certain genes — the study of these molecular factors is known as “epigenetics.” For example, every cell in a human fetus has the same DNA, but this DNA can develop into heart tissue, brain tissue, skin, liver, etc., depending on which genes are expressed and which genes are suppressed. The molecular factors responsible for gene expression are largely proteins, and these epigenetic factors can result in heritable changes in response to environmental conditions that are definitely not random.

The water flea, for example, can come in different variations, despite the same DNA, in response to the environmental conditions of the mother flea. If the mother flea experienced a large predator threat, the children of that flea would develop a spiny helmet for protection; otherwise the children would develop normal helmet-less heads. Studies have found that in other creatures, a particular diet can turn certain genes on or off, modifying offspring without changing DNA. In one study, mice that exercised not only enhanced their brain function, their children had enhanced brain function as well, though the effect only lasted one generation if exercise stopped. The Mexican cave fish once had eyes, but in its new dark environment, epigenetics has been responsible for turning off the genes responsible for eye development; its original DNA has been unchanged. (The hypothesized reason for this is that organisms tend to discard traits that are not needed in order to conserve energy.)

Recent studies of human beings have uncovered epigenetic adaptations that have allowed humans to flourish in such varied environments as deserts, jungles, and polar ice. The Oromo people of Ethiopia, recent settlers to the highlands of that country, have had epigenetic changes to their immune system to cope with new microbiological threats. Other populations in Africa have genetic mutations that have the twin effect of protecting against malaria but causing sickle cell anemia — recently it has been found that these mutations are being silenced in the face of declining malarial threats.  Increasingly, scientists are recognizing the large role of epigenetics in the evolution of human beings:

By encouraging the variations and adaptability of our species, epigenetic mechanisms for controlling gene expression have ensured that humanity could survive and thrive in any number of environments. Epigenetics is a significant part of the reason our species has become so adaptable, a trait that is often thought to distinguish us from what we often think of as lesser-evolved and developed animals that we inhabit this earth with. Indeed, it can be argued that epigenetics is responsible for, and provided our species with, the tools that truly made us unique in our ability to conquer any habitat and adapt to almost any climate. (Bioscience Horizons, 1 January 2017)

In fact, despite the hopes of scientists everywhere that the DNA sequencing of the human genome would provide a comprehensive biological explanation of human traits, it has been found that epigenetics may play a larger role in the complexity of human beings than the number of genes. According to one researcher, “[W]e found out that the human genome is probably not as complex and doesn’t have as many genes as plants do. So that, then, made us really question, ‘Well, if the genome has less genes in this species versus this species, and we’re more complex potentially, what’s going on here?'”

One additional nonrandom factor in evolution should be noted: the role of cooperation between organisms, which may even lead to biological mergers that create a new organism. Traditionally, evolution has been thought of primarily as random changes in organisms followed by a struggle for existence between competing organisms. It is a dark view of life. But increasingly, biologists have discovered that cooperation between organisms, known as symbiosis, also plays a role in the evolution of life, including the evolution of human beings.

Why was the role of cooperation in evolution overlooked until relatively recently? A number of biologists have argued that the society and culture of Darwin’s time played a significant role in shaping his theory — in particular, Adam Smith’s book The Wealth of Nations. In Smith’s view, the basic unit of economics was the self-interested individual on the marketplace, who bought and sold goods without any central planner overseeing his activities. Darwin essentially adopted this view and applied it to biological organisms: as businesses competed on the marketplace and flourished or died depending on how efficient they were, so too did organisms struggle against each other, with only the fittest surviving.

However, even in the late nineteenth century, a number of biologists noted cases in nature in which cooperation played a prominent role in evolution. In the 1880s, the Scottish biologist Patrick Geddes proposed that the reason the giant green anemone contained algal (algae) cells as well as animal cells was because of the evolution of a cooperative relationship between the two types of cells that resulted in a merger in which the alagal cells were merged into the animal flesh of the anemone. In the latter part of the twentieth century, biologist Lynn Margulis carried this concept further. Margulis argued that the most fundamental building block of advanced organisms, the cell, was the result of a merger between more primitive bacteria billions of years ago. By merging, each bacterium lent a particular biological advantage to the other, and created a more advanced life form. This theory was regarded with much skepticism at the time it was proposed, but over time it became widely accepted. The traditional picture of evolution as one in which new species diverge from older species and compete for survival has had to be supplemented with the picture of cooperative behavior and mergers. As one researcher has argued, “The classic image of evolution, the tree of life, almost always exclusively shows diverging branches; however, a banyan tree, with diverging and converging branches is best.”

More recent studies have demonstrated the remarkable level of cooperation between organisms that is the basis for human life. One study from a biologist at the University of Cambridge has proposed that human beings have as many as 145 genes that have been borrowed from bacteria, other single-celled organisms, and viruses. In addition, only about half of the human body is made up of human cells — the other half consists of trillions of microbes and quadrillions of viruses that largely live in harmony with human cells. Contrary to the popular view that microbes and viruses are threats to human beings, most of these microbes and viruses are harmless or even beneficial to humans. Microbes are essential in digesting food and synthesizing vitamins, and even the human immune system is partly built and partly operated by microbes! If, as one biologist has argued, each human being is a “society of cells,” it would be equally valid to describe a human being as a “society of cells and microbes.”

Is there randomness in evolution? Certainly. But the randomness is limited in scope, it takes place within a larger order which preserves incremental gains, and it provides the experimentation and diversity organisms need to meet new challenges and new environments. Alongside this randomness are epigenetic adaptations that turn genes on or off in response to environmental influences and the cooperative relations of symbiosis, which can build larger and more complex organisms. These additional facts do not prove the existence of a creator-God that oversees all of creation down to the most minute detail; but they do suggest a purposive order within which an astonishing variety of life forms can emerge and grow.

 

Review of “Modern Physics and Ancient Faith,” by Stephen Barr

Posted on by

I recently came across the book Modern Physics and Ancient Faith by Stephen Barr, a professor of physics at the University of Delaware. First published in 2003, the book was reprinted in 2013 by the University of Notre Dame press. I was initially skeptical of this book because reviews and praise for the book seemed to be limited mostly to religious and conservative publications. But after reading it, I have to say that the science in the book is solid, the author is reasonably open-minded, and the paucity of reviews of this book in scientific publications more likely reflects an unthinking prejudice rather than an informed judgment by scientists.

Modern Physics and Ancient Faith is not one of those books that attempts to prove the existence of God scientifically, an impossible task in any event. The book does show that belief in God is reasonable, that faith is not wholly irrational. But the main theme of the book is a critique of “scientific materialism,” a philosophy that emerged out of the scientific findings of the nineteenth century. What is “scientific materialism”? Barr summarizes the viewpoint as follows:

‘The universe more and more appears to be a vast, cold, blind, and pur­poseless machine. For a while it appeared that some things might escape the iron grip of science and its laws —perhaps Life or Mind. But the processes of life are now known to be just chemical reactions, involving the same ele­ments and the same basic physical laws that govern the behavior of all matter. The mind itself is, according to the overwhelming consensus of cognitive scientists, completely explicable as the performance of the biochemical computer called the brain. There is nothing in principle that a mind does which an artificial machine could not do just as well or even better. . . .

‘There is no evidence of a spiritual realm, or that God or souls are real. In fact, even if there did exist anything of a spiritual nature, it could have no influence on the visible world, because the material world is a closed sys­tem of physical cause and effect. Nothing external to it could affect its opera­tions without violating the precise mathematical relationships imposed by the laws of physics. . . .

‘All, therefore, is matter: atoms in ceaseless, aimless motion. In the words of Democritus, everything consists of’atoms and the void.’ Because the ulti­mate reality is matter, there cannot be any cosmic purpose or meaning, for atoms have no purposes or goals. . . .

‘Science has dethroned man. Far from being the center of things, he is now seen to be a very peripheral figure indeed. . . .  The human species is just one branch on an ancient evolutionary tree, and not so very different from some of the other branches—genetically we overlap more than 98 percent with chimpanzees. We are the product not of purpose, but of chance mutations. Bertrand Russell perfectly summed up man’s place in the cosmos when he called him ‘a curious accident in a backwater.” (pp. 19-20)

A great many educated people subscribe to many or most of these principles of scientific materialism. However, as Barr notes, these principles are based largely on scientific findings from the nineteenth century, and there have been a number of major advances in knowledge since then that have cast doubt on the principles of materialism. Barr refers to these newer findings as “plot twists.”

The first plot twist Barr notes is the “Big Bang” theory of the origins of the universe, first proposed in 1927 by Georges Lemaître, a Catholic priest and astronomer. Although taken for granted today, Lemaître’s idea of a universe emerging from a single, tiny point of concentrated energy was initially shocking and disturbing to many scientists. The predominant view of scientists for a number of centuries was that the universe existed eternally, with no beginning and no end. Even Einstein was disturbed by the Big Bang theory and thought it “abominable”; it took many years for him to accept it. I initially was skeptical of Barr’s claim that atheists and materialists were particularly disturbed by and opposed to the Big Bang, but a recent book on theories of the universe’s origins supports Barr’s claim (pp. 25-27).

Now it’s true that the Big Bang in itself doesn’t prove the existence of a creator. And there are many features of the universe which seem to argue against the idea of an omniscient and omnipotent creator, most prominently, the very gradual process of evolution, with its randomness and mass extinctions. Also, Georges Lemaître himself cautioned against any attempts to draw theological conclusions from his scientific work, and argued against the mixing of science and religion. Nevertheless, I don’t think it can be denied that the Big Bang is more compatible with the idea of a creator than the previously dominant theory of the eternal universe.

The second plot twist, according to Barr, is the gradual discovery of a deeper underlying harmony and beauty in the laws of physics, which suggest not blind and impersonal forces but a cosmic designer. Any one particular phenomenon can be explained by an impersonal law or mechanism, notes Barr; but when one looks at the structure of the universe as a whole, the question of a designer is “inescapable.” (Barr, p. 24) In addition, the story of the universe is not one of order emerging out of disorder or chaos, but rather order emerging out of a deeper order, rooted in mathematical structures and physical laws. Barr discusses a number of examples of this harmony and beauty, including symmetrical structures in nature, the growth of crystals, orbital ellipses, and particular mathematical equations that are simple yet also capable of resulting in highly complex orders.

I found this part of Barr’s book to be the least convincing. Symmetry in itself does not strike me as being particularly beautiful, though beautiful things may have symmetry as one of their properties. Furthermore, there are aspects of the universe that are definitely not beautiful, harmonious, or elegant, but rather messy, complicated, and wasteful. Elegance is something rightly valued by scientists, but there is no reason to believe that the underlying structure of nature is always fundamentally elegant, and scientists have sometimes been misguided into coming up with elegant solutions for phenomena that later turned out to be far messier and more complicated in reality. 

The third “plot twist” Barr discusses is, in my view, far more interesting and convincing: the discovery of “anthropic coincidences,” that is, features of the universe that suggest that the emergence of life, including intelligent life, is not an accident but is actually a predictable feature of the universe, built right into the structure. Barr accepts the theory of evolution and acknowledges that random mutations play a large role in the evolution of life (though he is skeptical that natural selection provides a complete explanation for the evolution of life). But Barr also argues that evolution proceeds from the foundation of a cosmic order which seems to be custom-made for the emergence of life. A good number of physical properties of the universe — the strong nuclear force, the creation of new elements through nuclear fusion, the stability of the proton, the strength of the electro-magnetic force, and other properties and processes — seem to be finely tuned to within a very narrow range of precision. Action outside the these strict boundaries of behavior set by the physical laws and constants of the universe would eliminate the possibility of life anywhere in the universe or even cause the universe to self-destruct. Again, these “anthropic coincidences” do not prove the existence of God, but they do seem to indicate that life is not just an accident of the universe, but an outcome built into the universe from the very beginning.

Barr acknowledges the argument of some physicists that the universe could well have different domains with different physical laws, or there could even be a large (or infinite) number of universes (the “multiverse”), each with a slightly different set of laws and constants. In this view, life only seems inevitable because we just happen to exist in a universe that has the right balance of laws and constants, and if the universe did not have this balance, no one would be there to observe that fact! But Barr is rightly skeptical of this argument, noting that it relies merely upon speculation, with no actual empirical evidence of other universes. If belief in God is unscientific because God is unobservable, then belief in an unobservable multiverse is also unscientific.

Barr devotes most of the remaining chapters of his book to refuting the scientific materialist view of humanity. In the materialist view, human beings are nothing more than biological mechanisms, made up of the same atoms that make up the rest of the universe, and therefore as determined and predictable as any other object in the universe. Humans have no soul apart from the body, no mind apart from the brain, and no real free will. Therefore, there is no reason to expect that artificial intelligence in advanced computers will be any different from human minds, aside from being superior. Barr rightly criticizes this view as the fallacy of reductionism, the notion that everything can be explained by reference to the parts that compose it. The problem with this view, as I have pointed out elsewhere, is that when parts join together, the resulting whole may be an entirely new phenomenon, with radically different properties from the parts.

Barr argues that although human beings may be made of materials, humans beings also have a spiritual side, defined as the possession of two crucial attributes: (1) an intellect capable of understanding; and (2) free will. As such, human beings are capable of transcending themselves, that is, go beyond their immediate desires and appetites, “perceive what is objectively true and beautiful,” (p. 168) and to freely choose good or evil.

It is precisely this quality of human beings that makes humans different from material objects, including computers. Barr points out that a computer can manipulate numbers and symbols, and do so much more quickly and efficiently than humans. But, he asks, in what way does a computer actually understand what it is doing? When you use a computer to calculate the sum of all annual profits for Corporation X, does the computer have any idea of what it is really doing? No — it is manipulating numbers and symbols, for the benefit of human beings who actually do have understanding. Likewise, the very notion of moral judgment and blame makes no sense when applied to a computer, because in practice we know that a computer does not have real understanding. In Barr’s words:

We do not really ‘blame’ a computer program for what it does; if anything, we blame its human programmers. We do not condemn a man-eating tiger, in the moral sense, or grow indignant at the typhoid bacillus. And yet we do feel that human beings can ‘deserve’ and that their behavior can be morally judged. We believe this precisely because we believe that human beings can make free choices. (p. 186)

More importantly, as Barr notes, the scientific materialist view of human beings as nothing more than machines is derived from scientific findings in earlier centuries, when scientists became increasingly capable of predicting the motions and actions of objects, large and small. Since human beings were nothing more than collections of material objects known as atoms, it stood to reason that human beings were also nothing more than predictable and determined in their actions. But early twentieth century research into the behavior of subatomic particles, known as “quantum physics,” overturned the view that the behavior of all objects could be predicted on the basis of predetermined laws of behavior. Rather, at the subatomic level, the behavior of objects were probabilistic, not determined; furthermore, the behavior of the particles could not be known until they interacted with an observer!

Today, it is widely acknowledged among scientists that the nineteenth century dream of a completely determined and predictable universe is an illusion, that the behavior of large solar, planetary, and sub-planetary bodies can be predicted to a large extent, but that other phenomenon remain less amenable to such study. Yet the materialist view of human beings as completely determined remains popular among many, including scientists who should know better. Barr rightly criticizes this view, noting that while quantum physics doesn’t prove that humans have free will, it does demolish the notion of complete determinism, and at the very least, creates space for free will.

However, while Barr effectively demolishes the scientific materialist view of human nature, I don’t think he demonstrates that the traditional Judeo-Christian view is entirely correct either. In this view, human beings have a soul that exists, or can exist, separately from the body, and this soul is imparted to human beings by God in a special act of creation. (p. 225) But rather than surmise that there is a separate spirit that possesses the material body and gives it life and understanding and free will, I think it makes more sense to adopt the outlook of theorists of emergence, that the correct combination and organization of parts can lead to the emergence of a whole organism that possesses life and understanding and free will, even if the parts themselves do not possess these qualities.

Another way to look at this issue is to carefully reexamine the whole notion of what “matter” is. Materialists conceive of humans as beings composed of collections of objects called atoms and can’t conceive how this collection of objects can possibly have understanding and free will. But human beings are not just made up of objects — we are beings of matter and energy. Physicists have defined “energy” as the capacity to do work, and if you think of human beings as collections of matter and energy, the attributes of life and understanding and free will no longer seem so mysterious: these attributes are synergistic expressions of a highly complex matter/energy combination.

One could go even further. Physicists have long noted that matter and energy are interchangeable, that matter can be transformed into energy and energy can be transformed into matter. According to the great physicist Werner Heisenberg, “[E]xperiments have shown the complete mutability of matter. All the elementary particles can, at sufficiently high energies, be transmuted into other particles, or they can simply be created from kinetic energy and can be annihilated into energy, for instance into radiation.” (Physics and Philosophy, p. 139.) In fact, the universe in its earliest stages began simply as energy and only gradually transformed some of that energy into matter, so even matter itself can be considered a form of condensed energy rather than a separate and unique entity. So you could think of humans as beings of energy, not just collections of objects — in which case consciousness and free will no longer seem so strange.

Overall, I think Barr’s book is largely convincing in his critique of scientific materialism. He does not provide scientific evidence for the existence of God, but he does make belief in God reasonable, as long as it is not a fundamentalist God. Indeed, any respectable book on science and religion is going to have to reject the notion that the Bible is literally true in all aspects if it is going to be properly scientific. I think Barr does occasionally engage in cherry-picking of evidence from religious thinkers and traditions that make it look as if early Jewish and Christian thinkers were more farsighted in their understanding of the universe than they actually were. But ultimately, judging a religion by its understanding of natural causation is a risky task; when new discoveries are made that overturn the old claims, what does one do? It would be absurd to deny the new discoveries in order to save the religion.

Religious knowledge should be considered primarily a form of transcendent knowledge about the Good, not empirical knowledge about what and how the world is. The Catholic priest-astronomer Georges Lemaître was correct in rejecting attempts by others to use his Big Bang theory as evidence for the merits of Christianity. The best test of a religion is not whether it explains nature, but whether it actually makes human beings and human civilization better.

Zen and the Art of Science: A Tribute to Robert Pirsig

Posted on by

Author Robert Pirsig, widely acclaimed for his bestselling books, Zen and the Art of Motorcycle Maintenance (1974) and Lila (1991), passed away in his home on April 24, 2017. A well-rounded intellectual equally at home in the sciences and the humanities, Pirsig made the case that scientific inquiry, art, and religious experience were all particular forms of knowledge arising out of a broader form of knowledge about the Good or what Pirsig called “Quality.” Yet, although Pirsig’s books were bestsellers, contemporary debates about science and religion are oddly neglectful of Pirsig’s work. So what did Pirsig claim about the common roots of human knowledge, and how do his arguments provide a basis for reconciling science and religion?

Pirsig gradually developed his philosophy as response to a crisis in the foundations of scientific knowledge, a crisis he first encountered while he was pursuing studies in biochemistry. The popular consensus at the time was that scientific methods promised objectivity and certainty in human knowledge. One developed hypotheses, conducted observations and experiments, and came to a conclusion based on objective data. That was how scientific knowledge accumulated.

However, Pirsig noted that, contrary to his own expectations, the number of hypotheses could easily grow faster than experiments could test them. One could not just come up with hypotheses – one had to make good hypotheses, ones that could eliminate the need for endless and unnecessary observations and testing. Good hypotheses required mental inspiration and intuition, components that were mysterious and unpredictable.  The greatest scientists were precisely like the greatest artists, capable of making immense creative leaps before the process of testing even began.  Without those creative leaps, science would remain on a never-ending treadmill of hypothesis development – this was the “infinity of hypotheses” problem.  And yet, the notion that science depended on intuition and artistic leaps ran counter to the established view that the scientific method required nothing more than reason and the observation and recording of an objective reality.

Consider Einstein. One of history’s greatest scientists, Einstein hardly ever conducted actual experiments. Rather, he frequently engaged in “thought experiments,” imagining what it would be like to chase a beam of light, what it would feel like to be in a falling elevator, and what a clock would look like if the streetcar he was riding raced away from the clock at the speed of light.

One of the most fruitful sources of hypotheses in science is mathematics, a discipline which consists of the creation of symbolic models of quantitative relationships. And yet, the nature of mathematical discovery is so mysterious that mathematicians themselves have compared their insights to mysticism. The great French mathematician Henri Poincare believed that the human mind worked subliminally on problems, and his work habit was to spend no more than two hours at a time working on mathematics. Poincare believed that his subconscious would continue working on problems while he conducted other activities, and indeed, many of his great discoveries occurred precisely when he was away from his desk. John von Neumann, one of the best mathematicians of the twentieth century, also believed in the subliminal mind. He would sometimes go to sleep with a mathematical problem on his mind and wake up in the middle of the night with a solution. The Indian mathematical genius Srinivasa Ramanujan was a Hindu mystic who believed that solutions were revealed to him in dreams by the goddess Namagiri.

Intuition and inspiration were human solutions to the infinity-of-hypotheses problem. But Pirsig noted there was a related problem that had to be solved — the infinity of facts.  Science depended on observation, but the issue of which facts to observe was neither obvious nor purely objective.  Scientists had to make value judgments as to which facts were worth close observation and which facts could be safely overlooked, at least for the moment.  This process often depended heavily on an imprecise sense or feeling, and sometimes mere accident brought certain facts to scientists’ attention. What values guided the search for facts? Pirsig cited Poincare’s work The Foundations of Science. According to Poincare, general facts were more important than particular facts, because one could explain more by focusing on the general than the specific. Desire for simplicity was next – by beginning with simple facts, one could begin the process of accumulating knowledge about nature without getting bogged down in complexity at the outset. Finally, interesting facts that provided new findings were more important than facts that were unimportant or trivial. The point was not to gather as many facts as possible but to condense as much experience as possible into a small volume of interesting findings.

Research on the human brain supports the idea that the ability to value is essential to the discernment of facts.  Professor of Neuroscience Antonio Damasio, in his book Descartes’ Error: Emotion, Reason, and the Human Brain, describes several cases of human beings who lost the part of their brain responsible for emotions, either because of an accident or a brain tumor.  These persons, some of whom were previously known as shrewd and smart businessmen, experienced a serious decline in their competency after damage took place to the emotional center of their brains.  They lost their capacity to make good decisions, to get along with other people, to manage their time, or to plan for the future.  In every other respect, these persons retained their cognitive abilities — their IQs remained above normal and their personality tests resulted in normal scores.  The only thing missing was their capacity to have emotions.  Yet this made a huge difference.  Damasio writes of one subject, “Elliot”:

Consider the beginning of his day: He needed prompting to get started in the morning and prepare to go to work.  Once at work he was unable to manage his time properly; he could not be trusted with a schedule.  When the job called for interrupting an activity and turning to another, he might persist nonetheless, seemingly losing sight of his main goal.  Or he might interrupt the activity he had engaged, to turn to something he found more captivating at that particular moment.  Imagine a task involving reading and classifying documents of a given client.  Elliot would read and fully understand the significance of the material, and he certainly knew how to sort out the documents according to the similarity or disparity of their content.  The problem was that he was likely, all of a sudden, to turn from the sorting task he had initiated to reading one of those papers, carefully and intelligently, and to spend an entire day doing so.  Or he might spend a whole afternoon deliberating on which principle of categorization should be applied: Should it be date, size of document, pertinence to the case, or another?   The flow of work was stopped. (p. 36)

Why did the loss of emotion, which might be expected to improve decision-making by making these persons coldly objective, result in poor decision-making instead?  According to Damasio, without emotions, these persons were unable to value, and without value, decision-making in the face of infinite facts became hopelessly capricious or paralyzed, even with normal or above-normal IQs.  Damasio noted, “the cold-bloodedness of Elliot’s reasoning prevented him from assigning different values to different options, and made his decision-making landscape hopelessly flat.” (p. 51) Damasio discusses several other similar case studies.

So how would it affect scientific progress if all scientists were like the subjects Damasio studied, free of emotion, and therefore, hypothetically capable of perfect objectivity?  Well it seems likely that science would advance very slowly, at best, or perhaps not at all.  After all, the same tools for effective decision-making in everyday life are needed for the scientific enterprise as well. A value-free scientist would not only be unable to sustain the social interaction that science requires, he or she would be unable to develop a research plan, manage his or her time, or stick to a research plan.

_________

Where Pirsig’s philosophy becomes particularly controversial and difficult to understand is in his approach to the truth. The dominant view of truth today is known as the “correspondence” theory of truth – that is, any human statement that is true must correspond precisely to something objectively real. In this view, the laws of physics and chemistry are real because they correspond to actual events that can be observed and demonstrated. Pirsig argues on the contrary that in order to understand reality, human beings must invent symbolic and conceptual models, that there is a large creative component to these models (it is not just a matter of pure correspondence to reality), and that multiple such models can explain the same reality even if they are based on wholly different principles. Math, logic, and even the laws of physics are not “out there” waiting to be discovered – they exist in the mind, which doesn’t mean that these things are bad or wrong or unreal.

There are several reasons why our symbolic and conceptual models don’t correspond literally to reality, according to Pirsig. First, there is always going to be a gap between reality and the concepts we use to describe reality, because reality is continuous and flowing, while concepts are discrete and static. The creation of concepts necessarily calls for cutting reality into pieces, but there is no one right way to divide reality, and something is always lost when this is done. In fact, Pirsig noted, our very notions of subjectivity and objectivity, the former allegedly representing personal whims and the latter representing truth, rested upon an artificial division of reality into subjects and objects; in fact, there were other ways of dividing reality that could be just as legitimate or useful. In addition, concepts are necessarily static – they can’t be always changing or we would not be able to make sense of them. Reality, however, is always changing. Finally, describing reality is not always a matter of using direct and literal language but may require analogy and imaginative figures of speech.

Because of these difficulties in expressing reality directly, a variety of symbolic and conceptual models, based on widely varying principles, are not only possible but necessary – necessary for science as well as other forms of knowledge. Pirsig points to the example of the crisis that occurred in mathematics in the nineteenth century. For many centuries, it was widely believed that geometry, as developed by the ancient Greek mathematician Euclid, was the most exact of all of the sciences.  Based on a small number of axioms from which one could deduce multiple propositions, Euclidean geometry represented a nearly perfect system of logic.  However, while most of Euclid’s axioms were seemingly indisputable, mathematicians had long experienced great difficulty in satisfactorily demonstrating the truth of one of the chief axioms on which Euclidean geometry was based. This slight uncertainty led to an even greater crisis of uncertainty when mathematicians discovered that they could reverse or negate this axiom and create alternative systems of geometry that were every bit as logical and valid as Euclidean geometry.  The science of geometry was gradually replaced by the study of multiple geometries. Pirsig cited Poincare, who pointed out that the principles of geometry were not eternal truths but definitions and that the test of a system of geometry was not whether it was true but how useful it was.

So how do we judge the usefulness or goodness of our symbolic and conceptual models? Traditionally, we have been told that pure objectivity is the only solution to the chaos of relativism, in which nothing is absolutely true. But Pirsig pointed out that this hasn’t really been how science has worked. Rather, models are constructed according to the often competing values of simplicity and generalizability, as well as accuracy. Theories aren’t just about matching concepts to facts; scientists are guided by a sense of the Good (Quality) to encapsulate as much of the most important knowledge as possible into a small package. But because there is no one right way to do this, rather than converging to one true symbolic and conceptual model, science has instead developed a multiplicity of models. This has not been a problem for science, because if a particular model is useful for addressing a particular problem, that is considered good enough.

The crisis in the foundations of mathematics created by the discovery of non-Euclidean geometries and other factors (such as the paradoxes inherent in set theory) has never really been resolved. Mathematics is no longer the source of absolute and certain truth, and in fact, it never really was. That doesn’t mean that mathematics isn’t useful – it certainly is enormously useful and helps us make true statements about the world. It’s just that there’s no single perfect and true system of mathematics. (On the crisis in the foundations of mathematics, see the papers here and here.) Mathematical axioms, once believed to be certain truths and the foundation of all proofs, are now considered definitions, assumptions, or hypotheses. And a substantial number of mathematicians now declare outright that mathematical objects are imaginary, that particular mathematical formulas may be used to model real events and relationships, but that mathematics itself has no existence outside the human mind. (See The Mathematical Experience by Philip J. Davis and Reuben Hersh.)

Even some basic rules of logic accepted for thousands of years have come under challenge in the past hundred years, not because they are absolutely wrong, but because they are inadequate in many cases, and a different set of rules is needed. The Law of the Excluded Middle states that any proposition must be either true or false (“P” or “not P” in symbolic logic). But ever since mathematicians discovered propositions which are possibly true but not provable, a third category of “possible/unknown” has been added. Other systems of logic have been invented that use the idea of multiple degrees of truth, or even an infinite continuum of truth, from absolutely false to absolutely true.

The notion that we need multiple symbolic and conceptual models to understand reality remains controversial to many. It smacks of relativism, they argue, in which every person’s opinion is as valid as another person’s. But historically, the use of multiple perspectives hasn’t resulted in the abandonment of intellectual standards among mathematicians and scientists. One still needs many years of education and an advanced degree to obtain a job as a mathematician or scientist, and there is a clear hierarchy among practitioners, with the very best mathematicians and scientists working at the most prestigious universities and winning the highest awards. That is because there are still standards for what is good mathematics and science, and scholars are rewarded for solving problems and advancing knowledge. The fact that no one has agreed on what is the One True system of mathematics or logic isn’t relevant. In fact, physicist Stephen Hawking has argued:

[O]ur brains interpret the input from our sensory organs by making a model of the world. When such a model is successful at explaining events, we tend to attribute to it, and to the elements and concepts that constitute it, the quality of reality or absolute truth. But there may be different ways in which one could model the same physical situation, with each employing different fundamental elements and concepts. If two such physical theories or models accurately predict the same events, one cannot be said to be more real than the other; rather we are free to use whichever model is more convenient (The Grand Design, p. 7).

Among the most controversial and mind-bending claims Pirsig makes is that the very laws of nature themselves exist only in the human mind. “Laws of nature are human inventions, like ghosts,” he writes. Pirsig even remarks that it makes no sense to think of the law of gravity existing before the universe, that it only came into existence when Isaac Newton thought of it. It’s an outrageous claim, but if one looks closely at what the laws of nature actually are, it’s not so crazy an argument as it first appears.

For all of the advances that science has made over the centuries, there remains a sharp division of views among philosophers and scientists on one very important issue: are the laws of nature actual causal powers responsible for the origins and continuance of the universe or are the laws of nature summary descriptions of causal patterns in nature? The distinction is an important one. In the former view, the laws of physics are pre-existing or eternal and possess god-like powers to create and shape the universe; in the latter view, the laws have no independent existence – we are simply finding causal patterns and regularities in nature that allow us to predict and we call these patterns “laws.”

One powerful argument in favor of the latter view is that most of the so-called “laws of nature,” contrary to the popular view, actually have exceptions – and sometimes the exceptions are large. That is because the laws are simplified models of real phenomena. The laws were cobbled together by scientists in order to strike a careful balance between the values of scope, predictive accuracy, and simplicity. Michael Scriven, a mathematician and philosopher at Claremont Graduate University, has noted that as a result of this balance of values, physical laws are actually approximations that apply only within a certain range. This point has also been made more recently by Ronald Giere, a professor of philosophy at the University of Minnesota, in Science Without Laws and Nancy Cartwright of the University of California at San Diego in How the Laws of Physics Lie.

Newton’s law of universal gravitation, for example, is not really universal. It becomes increasingly inaccurate under conditions of high gravity and very high velocities, and at the atomic level, gravity is completely swamped by other forces. Whether one uses Newton’s law depends on the specific conditions and the level of accuracy one requires. Newton’s laws of motion also have exceptions, depending on the force, distance, and speed. Kepler’s laws of planetary motion are an approximation based on the simplifying assumption of a planetary system consisting of one planet. The ideal gas law is an approximation which becomes inaccurate under conditions of low temperature and/or high pressure. The law of multiple proportions works for simple molecular compounds, but often fails for complex molecular compounds. Biologists have discovered so many exceptions to Mendel’s laws of genetics that some believe that Mendel’s laws should not even be considered laws.

So if we think of laws of nature as being pre-existing, eternal commandments, with god-like powers to shape the universe, how do we account for these exceptions to the laws? The standard response by scientists is that their laws are simplified depictions of the real laws. But if that is the case, why not state the “real” laws? Because by the time we wrote down the real laws, accounting for every possible exception, we would have an extremely lengthy and detailed description of causation that would not recognizably be a law. The whole point of the laws of nature was to develop tools by which one could predict a large number of phenomena (scope), maintain a good-enough correspondence to reality (accuracy), and make it possible to calculate predictions without spending an inordinate amount of time and effort (simplicity). That is why although Einstein’s conception of gravity and his “field equations” have supplanted Newton’s law of gravitation, physicists still use Newton’s “law” in most cases because it is simpler and easier to use; they only resort to Einstein’s complex equations when they have to! The laws of nature are human tools for understanding, not mathematical gods that shape the universe. The actual practice of science confirms Pirsig’s point that the symbolic and conceptual models that we create to understand reality have to be judged by how good they are – simple correspondence to reality is insufficient and in many cases is not even possible anyway.

_____________

 

Ultimately, Pirsig concluded, the scientific enterprise is not that different from the pursuit of other forms of knowledge – it is based on a search for the Good. Occasionally, you see this acknowledged explicitly, when mathematicians discuss the beauty of certain mathematical proofs or results, as defined by their originality, simplicity, ability to solve many problems at once, or their surprising nature. Scientists also sometimes write about the importance of elegance in their theories, defined as the ability to explain as much as possible, as clearly as possible, and as simply as possible. Depending on the field of study, the standards of judgment may be different, the tools may be different, and the scope of inquiry is different. But all forms of human knowledge — art, rhetoric, science, reason, and religion — originate in, and are dependent upon, a response to the Good or Quality. The difference between science and religion is that scientific models are more narrowly restricted to understanding how to predict and manipulate natural phenomena, whereas religious models address larger questions of meaning and value.

Pirsig did not ignore or suppress the failures of religious knowledge with regard to factual claims about nature and history. The traditional myths of creation and the stories of various prophets were contrary to what we know now about physics, biology, paleontology, and history. In addition, Pirsig was by no means a conventional theist — he apparently did not believe that God was a personal being who possessed the attributes of omniscience and omnipotence, controlling or potentially controlling everything in the universe.

However, Pirsig did believe that God was synonymous with the Good, or “Quality,” and was the source of all things.  In fact, Pirsig wrote that his concept of Quality was similar to the “Tao” (the “Way” or the “Path”) in the Chinese religion of Taoism. As such, Quality was the source of being and the center of existence. It was also an active, dynamic power, capable of bringing about higher and higher levels of being. The evolution of the universe, from simple physical forms, to complex chemical compounds, to biological organisms, to societies was Dynamic Quality in action. The most recent stage of evolution – Intellectual Quality – refers to the symbolic models that human beings create to understand the universe. They exist in the mind, but are a part of reality all the same – they represent a continuation of the growth of Quality.

What many religions were missing, in Pirsig’s view, was not objectivity, but dynamism: an ability to correct old errors and achieve new insights. The advantage of science was its willingness and ability to change. According to Pirsig,

If scientists had simply said Copernicus was right and Ptolemy was wrong without any willingness to further investigate the subject, then science would have simply become another minor religious creed. But scientific truth has always contained an overwhelming difference from theological truth: it is provisional. Science always contains an eraser, a mechanism whereby new Dynamic insight could wipe out old static patterns without destroying science itself. Thus science, unlike orthodox theology, has been capable of continuous, evolutionary growth. (Lila, p. 222)

The notion that religion and orthodoxy go together is widespread among believers and secularists. But there is no necessary connection between the two. All religions originate in social processes of story-telling, dialogue, and selective borrowing from other cultures. In fact, many religions begin as dangerous heresies before they become firmly established — orthodoxies come later. The problem with most contemporary understandings of religion is that one’s adherence to religion is often measured by one’s commitment to orthodoxy and membership in religious institutions rather than an honest quest for what is really good.  A person who insists on the literal truth of the Bible and goes to church more than once a week is perceived as being highly religious, whereas a person not connected with a church but who nevertheless seeks religious knowledge wherever he or she can find it is considered less committed or even secular.  This prejudice has led many young people to identify as “spiritual, not religious,” but religious knowledge is not inherently about unwavering loyalty to an institution or a text. Pirsig believed that mysticism was a necessary component of religious knowledge and a means of disrupting orthodoxies and recovering the dynamic aspect of religious insight.

There is no denying that the most prominent disputes between science and religion in the last several centuries regarding the physical workings of the universe have resulted in a clear triumph for scientific knowledge over religious knowledge.  But the solution to false religious beliefs is not to discard religious knowledge — religious knowledge still offers profound insights beyond the scope of science. That is why it is necessary to recover the dynamic nature of religious knowledge through mysticism, correction of old beliefs, and reform. As Pirsig argued, “Good is a noun.” Not because Good is a thing or an object, but because Good  is the center and foundation of all reality and all forms of knowledge, whether we are consciously aware of it or not.

What Does Science Explain? Part 5 – The Ghostly Forms of Physics

Posted on by

The sciences do not try to explain, they hardly even try to interpret, they mainly make models. By a model is meant a mathematical construct which, with the addition of certain verbal interpretations, describes observed phenomena. The justification of such a mathematical construct is solely and precisely that it is expected to work — that is, correctly to describe phenomena from a reasonably wide area. Furthermore, it must satisfy certain esthetic criteria — that is, in relation to how much it describes, it must be rather simple. — John von Neumann (“Method in the Physical Sciences,” in The Unity of Knowledge, 1955)

Now we come to the final part of our series of posts, “What Does Science Explain?” (If you have not already, you can peruse parts 1, 2, 3, and 4 here). As I mentioned in my previous posts, the rise of modern science was accompanied by a change in humanity’s view of metaphysics, that is, our theory of existence. Medieval metaphysics, largely influenced by ancient philosophers, saw human beings as the center or summit of creation; furthermore, medieval metaphysics proposed a sophisticated, multifaceted view of causation. Modern scientists, however, rejected much of medieval metaphysics as subjective and saw reality as consisting mainly of objects impacting or influencing each other in mathematical patterns.  (See The Metaphysical Foundations of Modern Science by E.A. Burtt.)

I have already critically examined certain aspects of the metaphysics of modern science in parts 3 and 4. For part 5, I wish to look more closely at the role of Forms in causation — what Aristotle called “formal causation.” This theory of causation was strongly influenced by Aristotle’s predecessor Plato and his Theory of Forms. What is Plato’s “Theory of Forms”? In brief, Plato argued that the world we see around us — including all people, trees, and animals, stars, planets and other objects — is not the true reality. The world and the things in it are imperfect and perishable realizations of perfect forms that are eternal, and that continually give birth to the things we see. That is, forms are the eternal blueprints of perfection which the material world imperfectly represents. True philosophers do not focus on the material world as it is, but on the forms that material things imperfectly reflect. In order to judge a sculpture, painting, or natural setting, a person must have an inner sense of beauty. In order to evaluate the health of a particular human body, a doctor must have an idea of what a perfectly healthy human form is. In order to evaluate a government’s system of justice, a citizen must have an idea about what perfect justice would look like. In order to critically judge leaders, citizens must have a notion of the virtues that such a leader should have, such as wisdom, honesty, and courage.  Ultimately, according to Plato, a wise human being must learn and know the perfect forms behind the imperfect things we see: we must know the Form of Beauty, the Form of Justice, the Form of Wisdom, and the ultimate form, the Form of Goodness, from which all other forms flow.

Unsurprisingly, many intelligent people in the modern world regard Plato’s Theory of Forms as dubious or even outrageous. Modern science teaches us that sure knowledge can only be obtained by observation and testing of real things, but Plato tells us that our senses are deceptive, that the true reality is hidden behind what we sense. How can we possibly confirm that the forms are real? Even Plato’s student Aristotle had problems with the Theory of Forms and argued that while the forms were real, they did not really exist until they were manifested in material things.

However, there is one important sense in which modern science retained the notion of formal causation, and that is in mathematics. In other words, most scientists have rejected Plato’s Theory of Forms in all aspects except for Plato’s view of mathematics. “Mathematical Platonism,” as it is called, is the idea that mathematical forms are objectively real and are part of the intrinsic order of the universe. However, there are also sharp disagreements on this subject, with some mathematicians and scientists arguing that mathematical forms are actually creations of the human imagination.

The chief difference between Plato and modern scientists on the study of mathematics is this: According to Plato, the objects of geometry — perfect squares, perfect circles, perfect planes — existed nowhere in the material world; we only see imperfect realizations. But the truly wise studied the perfect, eternal forms of geometry rather than their imperfect realizations. Therefore, while astronomical observations indicated that planetary bodies orbited in imperfect circles, with some irregularities and errors, Plato argued that philosophers must study the perfect forms instead of the actual orbits! (The Republic, XXVI, 524D-530C) Modern science, on the other hand, is committed to observation and study of real orbits as well as the study of perfect mathematical forms.

Is it tenable to hold the belief that Plato and Aristotle’s view of eternal forms is mostly subjective nonsense, but they were absolutely right about mathematical forms being real? I argue that this selective borrowing of the ancient Greeks doesn’t quite work, that some of the questions and difficulties with proving the reality of Platonic forms also afflicts mathematical forms.

The main argument for mathematical Platonism is that mathematics is absolutely necessary for science: mathematics is the basis for the most important and valuable physical laws (which are usually in the form of equations), and everyone who accepts science must agree that the laws of nature or the laws of physics exist. However, the counterargument to this claim is that while mathematics is necessary for human beings to conduct science and understand reality, that does not mean that mathematical objects or even the laws of nature exist objectively, that is, outside of human minds.

I have discussed some of the mysterious qualities of the “laws of nature” in previous posts (here and here). It is worth pointing out that there remains a serious debate among philosophers as to whether the laws of nature are (a) descriptions of causal regularities which help us to predict or (b) causal forces in themselves. This is an important distinction that most people, including scientists, don’t notice, although the theoretical consequences are enormous. Physicist Kip Thorne writes that laws “force the Universe to behave the way it does.” But if laws have that kind of power, they must be ubiquitous (exist everywhere), eternal (exist prior to the universe), and have enormous powers although they have no detectable energy or mass — in other words, the laws of nature constitute some kind of supernatural spirit. On the other hand, if laws are summary descriptions of causation, these difficulties can be avoided — but then the issue arises: do the laws of nature or of physics really exist objectively, outside of human minds, or are they simply human-constructed statements about patterns of causation? There are good reasons to believe the latter is true.

The first thing that needs to be said is that nearly all these so-called laws of nature are actually approximations of what really happens in nature, approximations that work only under certain restrictive conditions. Both of these considerations must be taken into account, because even the approximations fall apart outside of certain pre-specified conditions. Newton’s law of universal gravitation, for example, is not really universal. It becomes increasingly inaccurate under conditions of high gravity and very high velocities, and at the atomic level, gravity is completely swamped by other forces. Whether one uses Newton’s law depends on the specific conditions and the level of accuracy one requires. Kepler’s laws of planetary motion are an approximation based on the simplifying assumption of a planetary system consisting of one planet. The ideal gas law is an approximation which becomes inaccurate under conditions of low temperature and/or high pressure. The law of multiple proportions works for simple molecular compounds, but often fails for complex molecular compounds. Biologists have discovered so many exceptions to Mendel’s laws of genetics that some believe that Mendel’s laws should not even be considered laws.

The fact of the matter is that even with the best laws that science has come up with, we still can’t predict the motions of more than two interacting astronomical bodies without making unrealistic simplifying assumptions. Michael Scriven, a mathematician and philosopher at Claremont Graduate University, has concluded that the laws of nature or physics are actually cobbled together by scientists based on multiple criteria:

Briefly we may say that typical physical laws express a relationship between quantities or a property of systems which is the simplest useful approximation to the true physical behavior and which appears to be theoretically tractable. “Simplest” is vague in many cases, but clear for the extreme cases which provide its only use. “Useful” is a function of accuracy and range and purpose. (Michael Scriven, “The Key Property of Physical Laws — Inaccuracy,” in Current Issues in the Philosophy of Science, ed. Herbert Feigl)

The response to this argument is that it doesn’t disprove the objective existence of physical laws — it simply means that the laws that scientists come up with are approximations to real, objectively existing underlying laws. But if that is the case, why don’t scientists simply state what the true laws are? Because the “laws” would actually end up being extremely long and complex statements of causation, with so many conditions and exceptions that they would not really be considered laws.

An additional counterargument to mathematical Platonism is that while mathematics is necessary for science, it is not necessary for the universe. This is another important distinction that many people overlook. Understanding how things work often requires mathematics, but that doesn’t mean the things in themselves require mathematics. The study of geometry has given us pi and the Pythagorean theorem, but a child does not need to know these things in order to draw a circle or a right triangle. Circles and right triangles can exist without anyone, including the universe, knowing the value of pi or the Pythagorean theorem. Calculus was invented in order to understand change and acceleration; but an asteroid, a bird, or a cheetah is perfectly capable of changing direction or accelerating without needing to know calculus.

Even among mathematicians and scientists, there is a significant minority who have argued that mathematical objects are actually creations of the human imagination, that math may be used to model aspects of reality, but it does not necessarily do so. Mathematicians Philip J. Davis and Reuben Hersh argue that mathematics is the study of “true facts about imaginary objects.” Derek Abbot, a professor of engineering, writes that engineers tend to reject mathematical Platonism: “the engineer is well acquainted with the art of approximation. An engineer is trained to be aware of the frailty of each model and its limits when it breaks down. . . . An engineer . . . has no difficulty in seeing that there is no such a thing as a perfect circle anywhere in the physical universe, and thus pi is merely a useful mental construct.” (“The Reasonable Ineffectiveness of Mathematics“) Einstein himself, making a distinction between mathematical objects used as models and pure mathematics, wrote that “As far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality.” Hartry Field, a philosopher at New York University, has argued that mathematics is a useful fiction that may not even be necessary for science. Field goes to show that it is possible to reconstruct Newton’s theory of gravity without using mathematics. (There is more discussion on this subject here and here.)

So what can we conclude about the existence of forms? I have to admit that although I’m skeptical, I have no sure conclusions. It seems unlikely that forms exist outside the mind . . . but I can’t prove they don’t exist either. Forms do seem to be necessary for human reasoning — no thinking human can do without them. And forms seem to be rooted in reality: perfect circles, perfect squares, and perfect human forms can be thought of as imaginative projections of things we see, unlike Sherlock Holmes or fire-breathing dragons or flying spaghetti monsters, which are more creatively fictitious. Perhaps one could reconcile these opposing views on forms by positing that the human mind and imagination is part of the universe itself, and that the universe is becoming increasingly consciously aware.

Another way to think about this issue was offered by Robert Pirsig in Zen and the Art of Motorcycle Maintenance. According to Pirsig, Plato made a mistake by positing Goodness as a form. Even considered as the highest form, Goodness (or “Quality,” in Pirsig’s terminology) can’t really be thought of as a static thing floating around in space or some otherworldly realm. Forms are conceptual creations of humans who are responding to Goodness (Quality). Goodness itself is not a form, because it is not an unchanging thing — it is not static or even definable. It is “reality itself, ever changing, ultimately unknowable in any kind of fixed, rigid way.” (p. 342) Once we let go of the idea that Goodness or Quality is a form, we can realize that not only is Goodness part of reality, it is reality.

As conceptual creations, ideal forms are found in both science and religion. So why, then, does there seem to be such a sharp split between science and religion as modes of knowledge? I think it comes down to this: science creates ideal forms in order to model and predict physical phenomena, while religion creates ideal forms in order to provide guidance on how we should live.

Scientists like to see how things work — they study the parts in order to understand how the wholes work. To increase their understanding, scientists may break down certain parts into smaller parts, and those parts into even smaller parts, until they come to the most fundamental, indivisible parts. Mathematics has been extremely useful in modeling and understanding these parts of nature, so scientists create and appreciate mathematical forms.

Religion, on the other hand, tends to focus on larger wholes. The imaginative element of religion envisions perfect states of being, whether it be the Garden of Eden or the Kingdom of Heaven, as well as perfect (or near perfect) humans who serve as prophets or guides to a better life. Religion is less concerned with how things work than with how things ought to work, how things ought to be. So religion will tend to focus on subjects not covered by science, including the nature and meaning of beauty, love, and justice. There will always be debates about the appropriateness of particular forms in particular circumstances, but the use of forms in both science and religion is essential to understanding the universe and our place in it.

What Does Science Explain? Part 2 – The Metaphysics of Modern Science

Posted on by

In my previous post, I discussed the nature of metaphysics, a theory of being and existence, in the medieval world. The metaphysics of the medieval period was strongly influenced by the ancient Greeks, particularly Aristotle, who posited four causes or explanations for why things were. In addition, Aristotle argued that existence could be understood as the result of a transition from “potentiality” to “actuality.” With the rise of modern science, argued Edwin Arthur Burtt in The Metaphysical Foundations of Modern Science, the medieval conception of existence changed. Although some of this change was beneficial, argued Burtt, there was also a loss.

The first major change that modern science brought about was the strict separation of human beings, along with human senses and desires, from the “real” universe of impersonal objects joining, separating, and colliding with each other. Rather than seeing human beings as the center or summit of creation, as the medievals did, modern scientists removed the privileged position of human beings and promoted the goal of “objectivity” in their studies, arguing that we needed to dismiss all subjective human sensations and look at objects as they were in themselves. Kepler, Galileo, and Newton made a sharp distinction between the “primary qualities” of objects and “secondary qualities,” arguing that only primary qualities were truly real, and therefore worth studying. What were the “primary qualities?”: quantity/mathematics, motion, shape, and solidity. These qualities existed within objects and were independent of human perception and sensation. The “secondary qualities” were color, taste, smell, and sound; these were subjective because they were derived from human sensations, and therefore did not provide objective facts that could advance knowledge.

The second major change that modern science brought to metaphysics was a dismissal of the medieval world’s rich and multifaceted concept of causation in favor of a focus on “efficient causation” (the impact of one object or event on another). The concept of “final causation,” that is, goal-oriented development, was neglected. In addition, the concept of “formal causation,” that is, the emergence of things out of universal forms, was reduced to mathematics; only mathematical forms expressed in the “laws of nature,” were truly real, according to the new scientific worldview. Thus, all causation was reduced to mathematical “laws of nature” directing the motion and interaction of objects.

The consequences of this new worldview were tremendous in terms of altering humanity’s conception of reality and what it meant to explain reality. According to Burtt, “From now on, it is a settled assumption for modern thought in practically every field, that to explain anything is to reduce it to its elementary parts, whose relations, where temporal in character, are conceived in terms of efficient causality solely.” (Metaphysics of Modern Science, p. 134) And although the early giants of science — Kepler, Galileo, and Newton — believed in God, their conception of God was significantly different from the medieval view. Rather than seeing God as the Supreme Good, the goal or end which continually brought all things from potentiality to actuality, they saw God in terms of the “First Efficient Cause” only. That is, God brought the laws of nature into existence, and then the universe operated like a clock or machine, which might then only occasionally need rewinding or maintenance. But once this conception of God became widespread, it was not long before people questioned whether God was necessary at all to explain the universe.

Inarguably, there were great advantages to the metaphysical views of early scientists. By focusing on mathematical models and efficient causes, while pruning away many of the non-calculable qualities of natural phenomena, scientists were able to develop excellent predictive models. Descartes gave up the study of “final causes” and focused his energies on mathematics because he felt no one could discern God’s purposes, a view adopted widely by subsequent scientists. Both Galileo and Newton put great emphasis on the importance of observation and experimentation in the study of nature, which in many cases put an end to abstract philosophical speculations on natural phenomena that gave no definite conclusions. And Newton gave precise meanings to previously vague terms like “force” and “mass,” meanings that allowed measurement and calculation.

The mistake that these early scientists made, however, was to elevate a method into a metaphysics, by proclaiming that what they studied was the only true reality, with all else existing solely in the human mind. According to Burtt,

[T]he great Newton’s authority was squarely behind that view of the cosmos which saw in man a puny, irrelevant spectator . . . of the vast mathematical system whose regular motions according to mechanical principles constituted the world of nature. . . . The world that people had thought themselves living in — a world rich with colour and sound, redolent with fragrance, filled with gladness, love and beauty, speaking everywhere of purposive harmony and creative ideals — was crowded now into minute corners in the brains of scattered organic beings. The really important world outside was a world hard, cold, colourless, silent, and dead; a world of quantity, a world of mathematically computable motions in mechanical regularity.  (pp. 238-9)

Even at the time this new scientific metaphysics was being developed, it was critiqued on various grounds by philosophers such as Leibniz, Hume, and Berkeley. These philosophers’ critiques had little long-term impact, probably because scientists offered working predictive models and philosophers did not. But today, even as science is promising an eventual “theory of everything,” the limitations of the metaphysics of modern science is causing even some scientists to rethink the whole issue of causation and the role of human sensations in developing knowledge. The necessity for rethinking the modern scientific view of metaphysics will be the subject of my next post.

What Does Science Explain? Part 1 – What is Causation?

Posted on by

In previous posts, I have argued that science has been excellent at creating predictive models of natural phenomena. From the origins of the universe, to the evolution of life, to chemical reactions, and the building of technological devices, scientists have learned to predict causal sequences and manipulate these causal sequences for the benefit (or occasionally, detriment) of humankind. These models have been stupendous achievements of civilization, and religious texts and institutions simply cannot compete in terms of offering predictive models.

There remains the issue, however, of whether the predictive models of science really explain all that there is to explain. While many are inclined to believe that the models of science explain everything, or at least everything that one needs to know, there are actually some serious disputes even among scientists about what causation is, what a valid explanation is, whether predictive models need to be realistic, and how real are some of the entities scientists study, such as the “laws of nature” and the mathematics that are often part of those laws.

The fundamental issues of causation, explanation, and reality are discussed in detail in a book published in 1954 entitled: The Metaphysical Foundations of Modern Science by Edwin Arthur Burtt. According to Burtt, the birth and growth of modern science came with the development of a new metaphysics, that is, the study of being and existence. Copernicus, Kepler, Galileo, and Newton all played a role in creating this new metaphysics, and it shapes how we view the world to this day.

In order to understand Burtt’s thesis, we need to back up a bit and briefly discuss the state of metaphysics before modern science — that is, medieval metaphysics. The medieval view of the world in the West was based largely on Christianity and the ancient Greek philosophers such as Aristotle, who wrote treatises on both physics and metaphysics.

Aristotle wrote that there were four types of answers to the question “why?” These answers were described by Aristotle as the “four causes,” though it has been argued that the correct translation of the Greek word that Aristotle used is “explanation” rather than “cause.” These are:

(1) Material cause

(2) Formal cause

(3) Efficient (or moving) cause

(4) Final cause

“Material cause” refers to changes that take place as a result of the material that something is made of. If a substance melts at a particular temperature, one can argue that it is the material nature of that substance that causes it to melt at that temperature. (The problem with this kind of explanation is that it is not very deep — one can then ask why a material behaves as it does.)

“Formal cause” refers to the changes that take place in matter because of the form that an object is destined to have. According to Aristotle, all objects share the same matter — it is the arrangement of matter into their proper forms that causes matter to become a rock, a tree, a bird, or a human being. Objects and living things eventually disintegrate and perish, but the forms are eternal, and they shape matter into new objects and living things that replace the old. The idea of formal causation is rooted in Plato’s theory of forms, though Aristotle modified Plato’s theory in a number of ways.

“Efficient cause” refers to the change that takes place when one object impacts another; one object or event is the cause, the other is the effect. A stick hitting a ball, a saw cutting wood, and hydrogen atoms interacting with oxygen atoms to create water are all examples of efficient causes.

“Final cause” refers to the goal, end, or purpose of a thing — the Greek word for goal is “telos.” An acorn grows into an oak tree because that is the goal or telos of an acorn. Likewise, a fertilized human ovum becomes a human being. In nature, birds fly, rain nourishes plants, and the moon orbits the earth, because nature has intended certain ends for certain things. The concept of a “final cause” is intimately related to the “formal cause,” in the sense that the forms tend to provide the ends that matter pursues.

Related to these four causes or explanations is Aristotle’s notion of potentiality and actuality. Before things come into existence, one can say that there is potential; when these things come into existence they are actualized. Hydrogen atoms and oxygen atoms have the potential to become water if they are joined in the right way, but until they are so joined, there is only potential water, not actual water. A block of marble has the potential to become a statue, but it is not actually a statue until a sculptor completes his or her work. A human being is potentially wise if he or she pursues knowledge, but until that pursuit of knowledge is carried out, there is only potentiality and not actuality. The forms and telos of nature are primarily responsible for the transformation of potentiality into actuality.

Two other aspects of the medieval view of metaphysics are worth noting. First, for the medievals, human beings were the center of the universe, the highest end of nature. Stars, planets, trees, animals, chemicals, were lower forms of being than humans and existed for the benefit of humans. Second, God was not merely the first cause of the universe — God was the Supreme Good, the goal or telos to which all creation was drawn in pursuit of its final goals and perfection. According to Burtt,

When medieval philosophers thought of what we call the temporal process it was this continuous transformation of potentiality into actuality that they had in mind. . . . God was the One who eternally exists, and ever draws into movement by his perfect beauty all that is potentially the bearer of a higher existence. He is the divine harmony of all goods, conceived as now realized in ideal activity, eternally present, himself unmoved, yet the mover of all change. (Burtt, The Metaphysical Foundations of Modern Science, pp. 94-5)

The rise of modern science, according to Burtt, led to a radical change in humanity’s metaphysical views. A great deal of this change was beneficial, in the sense that it led to predictive models that successfully answered certain questions about natural processes that were previously mysterious. However, as Burtt noted, the new metaphysics of science was also a straitjacket that constricted humanity’s pursuit of knowledge. Some human senses were unjustifiably dismissed as unreliable or deceptive and some types of causation were swept away unnecessarily. How modern science created a new metaphysics that changed humanity’s conception of reality will be discussed in part two.

The Use of Fiction and Falsehood in Science

Posted on by

Astrophysicist Neil deGrasse Tyson has some interesting and provocative things to say about religion in a recent interview. I tend to agree with Tyson that religions have a number of odd or even absurd beliefs that are contrary to science and reason. One statement by Tyson, however, struck me as inaccurate. According to Tyson, “[T]here are religions and belief systems, and objective truths. And if we’re going to govern a country, we need to base that governance on objective truths — not your personal belief system.” (The Daily Beast)

I have a great deal of respect for Tyson as a scientist, and Tyson clearly knows more about physics than I do. But I think his understanding of what scientific knowledge provides is naïve and unsupported by history and present day practice. The fact of the matter is that scientists also have belief systems, “mental models” of how the world works. These mental models are often excellent at making predictions, and may also be good for explanation. But the mental models of science may not be “objectively true” in representing reality.

The best mental models in science satisfy several criteria: they reliably predict natural phenomena; they cover a wide range of such phenomena (i.e., they cover much more than a handful of special cases); and they are relatively simple. Now it is not easy to create a mental model that satisfies these criteria, especially because there are tradeoffs between the different criteria. As a result, even the best scientists struggle for many years to create adequate models. But as descriptions of reality, the models, or components of the models, may be fictional or even false. Moreover, although we think that the models we have today are true, every good scientist knows that in the future our current models may be completely overturned by new models based on entirely new conceptions. Yet in many cases, scientists often respect or retain the older models because they are useful, even if the models’ match to reality is false!

Consider the differences between Isaac Newton’s conception of gravity and Albert Einstein’s conception of gravity. According to Newton, gravity is a force that attracts objects to each other. If you throw a ball on earth, the path of the ball eventually curves downward because of the gravitational attraction of the earth. In Newton’s view, planets orbit the sun because the force of gravity pulls planetary bodies away from the straight line paths that they would normally follow as a result of inertia: hence, planets move in circular orbits. But according to Einstein, gravity is not a force — gravity seems like it’s a force, but it’s actually a “fictitious force.” In Einstein’s view, objects seem to attract each other because mass warps or curves spacetime, and objects tend to follow the paths made by curved spacetime. Newton and Einstein agree that inertia causes objects in motion to continue in straight lines unless they are acted on by a force; but in Einstein’s view, planets orbit the sun because they are actually already travelling straight paths, only in curved spacetime! (Yes this makes sense — if you travel in a jet, your straightest possible path between two cities is actually curved, because the earth is round.)

Scientists agree that Einstein’s view of gravity is correct (for now). But they also continue to use Newtonian models all the time. Why? Because Newtonian models are much simpler than Einstein’s and scientists don’t want to work harder than they have to! Using Newtonian conceptions of gravity as a real force, scientists can still track the paths of objects and send satellites into orbit; Newton’s equations work perfectly fine as predictive models in most cases. It is only in extraordinary cases of very high gravity or very high speeds that scientists must abandon Newtonian models and use Einstein’s to get more accurate predictions. Otherwise scientists much prefer to assume gravity is a real force and use Newtonian models. Other fictitious forces that scientists calculate using Newton’s models are the Coriolis force and centrifugal force.

Even in cases where you might expect scientists to use Einstein’s conception of curved spacetime, there is not a consistent practice. Sometimes scientists assume that spacetime is curved, sometimes they assume spacetime is flat. According to theoretical physicist Kip Thorne, “It is extremely useful, in relativity research, to have both paradigms at one’s fingertips. Some problems are solved most easily and quickly using the curved spacetime paradigm; others, using flat spacetime. Black hole problems . . . are most amenable to curved spacetime techniques; gravitational-wave problems . . . are most amenable to flat spacetime techniques.” (Black Holes and Time Warps). Whatever method provides the best results is what matters, not so much whether spacetime is really curved or not.

The question of the reality of mental models in science is particularly acute with regard to mathematical models. For many years, mathematicians have been debating whether or not the objects of mathematics are real, and they have yet to arrive at a consensus. So, if an equation accurately predicts how natural phenomena behave, is it because the equation exists “out there” someplace? Or is it because the equation is just a really good mental model? Einstein himself argued that “As far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality.” By this, Einstein meant that it was possible to create perfectly certain mathematical models in the human mind; but that the matching of these models’ predictions to natural phenomenon required repeated observation and testing, and one could never be completely sure that one’s model was the final answer and therefore that it really objectively existed.

And even if mathematical models work perfectly in predicting the behavior of natural phenomena, there remains the question of whether the different components of the model really match to something in reality. As noted above, Newton’s model of gravity does a pretty good job of predicting motion — but the part of the model that describes gravity as a force is simply wrong. In mathematics, the set of numbers known as “imaginary numbers” are used by engineers for calculating electric current; they are used by 3D modelers; and they are used by physicists in quantum mechanics, among other applications. But that doesn’t necessarily mean that imaginary numbers exist or correspond to some real quantity — they are just useful components of an equation.

A great many scientists are quite upfront about the fact that their models may not be an accurate reflection of reality. In their view, the purpose of science is to predict the behavior of natural phenomena, and as long as science gets better and better at this, it is less important if models are proved to be a mismatch to reality. Brian Koberlein, an astrophysicist at the Rochester Institute of Technology, writes that scientific theories should be judged by the quality and quantity of their predictions, and that theories capable of making predictions can’t be proved wrong, only replaced by theories that are better at predicting. For example, he notes that the caloric theory of heat, which posited the existence of an invisible fluid within materials, was quite successful in predicting the behavior of heat in objects, and still is at present. Today, we don’t believe such a fluid exists, but we didn’t discard the theory until we came up with a new theory that could predict better. The caloric theory of heat wasn’t “proven wrong,” just replaced with something better. Koberlein also points to Newton’s conception of gravity, which is still used today because it is simpler than Einstein’s and “good enough” at predicting in most cases. Koberlein concludes that for these reasons, Einstein will “never” be wrong — we just may find a theory better at predicting.

Stephen Hawking has discussed the problem of truly knowing reality, and notes that it perfectly possible to have different theories with entirely different conceptual frameworks that work equally well at predicting the same phenomena. In a fanciful example, Hawking notes that goldfish living in a curved bowl will see straight-line movement outside the bowl as being curved, but despite this it would still be possible for goldfish to develop good predictive theories. He notes that likewise, human beings may also have a distorted picture of reality, but we are still capable of building good predictive models. Hawking calls his philosophy “model-dependent realism”:

According to model-dependent realism, it is pointless to ask whether a model is real, only whether it agrees with observation. If there are two models that both agree with observation, like the goldfish’s model and ours, then one cannot say that one is more real than the other. One can use whichever model is more convenient in the situation under consideration. (The Grand Design, p. 46)

So if science consists of belief systems/mental models, which may contain fictions or falsehoods, how exactly does science differ from religion?

Well for one thing, science far excels religion in providing good predictive models. If you want to know how the universe began, how life evolved on earth, how to launch a satellite into orbit, or how to build a computer, religious texts offer virtually nothing that can help you with these tasks. Neil deGrasse Tyson is absolutely correct about the failure of religion in this respect.  Traditional stories of the earth’s creations, as found in the Bible’s book of Genesis, were useful first attempts to understand our origins, but they have been long-eclipsed by contemporary scientific models, and there is no use denying this.

What religion does offer, and science does not, is a transcendent picture of how we ought to live our lives and an interpretation of life’s meaning according to this transcendent picture. The behavior of natural phenomena can be predicted to some extent by science, but human beings are free-willed. We can decide to love others or love ourselves above others. We can seek peace, or murder in the pursuit of power and profit. Whatever we decide to do, science can assist us in our actions, but it can’t provide guidance on what we ought to do. Religion provides that vision, and if these visions are imaginative, so are many aspects of scientific models. Einstein himself, while insisting that science was the pursuit of objective knowledge, also saw a role for religion in providing a transcendent vision:

[T]he scientific method can teach us nothing else beyond how facts are related to, and conditioned by, each other.The aspiration toward such objective knowledge belongs to the highest of which man is capabIe, and you will certainly not suspect me of wishing to belittle the achievements and the heroic efforts of man in this sphere. Yet it is equally clear that knowledge of what is does not open the door directly to what should be. . . . Objective knowledge provides us with powerful instruments for the achievements of certain ends, but the ultimate goal itself and the longing to reach it must come from another source. . . .

To make clear these fundamental ends and valuations, and to set them fast in the emotional life of the individual, seems to me precisely the most important function which religion has to perform in the social life of man.

Now fundamentalists and atheists might both agree that rejecting the truth of sacred scripture with regard to the big bang and evolution tends to undermine the transcendent visions of religion. But the fact of the matter is that scientists never reject a mental model simply because parts of the model may be fictional or false; if the model provides useful guidance, it is still a valid part of human knowledge.

Does the Flying Spaghetti Monster Exist?

Posted on by

In a previous post, Belief and Evidence, I addressed the argument made by many atheists that those who believe in God have the burden of proof. In this view, evidence must accompany belief, and belief in anything for which there is insufficient evidence is irrational. One popular example cited by proponents of this view is the satirical creation known as the “Flying Spaghetti Monster.” Proposed as a response to the demands by creationists for equal time in the classroom with evolutionary theory, the Flying Spaghetti Monster has been cited as an example of an absurd entity which no one has the right to believe in unless one has actual evidence. According to famous atheist Richard Dawkins, disbelievers are not required to submit evidence against the existence of either God or the Flying Spaghetti Monster, it is believers that have the burden of proof.

The problem with this philosophy is that it would seem to apply equally well to many physicists’ theories of the “multiverse,” and in fact many scientists have criticized multiverse theories on the grounds that there is no way to observe or test for other universes. The most extreme multiverse theories propose that every mathematically possible universe, each with its own slight variation on physical laws and constants, exists somewhere. Multiverse theory has even led to bizarre speculations about hypothetical entities such as “Boltzmann brains.” According to some scientists, it is statistically more likely for the random fluctuations of matter to create a free-floating brain than it is for billions of years of universal evolution to lead to brains in human bodies. (You may have heard of the claim that a million monkeys typing on a million typewriters will eventually produce the works of Shakespeare — the principle is similar.) This means that reincarnation could be possible or that we are actually Boltzmann brains that were randomly generated by matter and that we merely have the illusion that we have bodies and an actual past. According to physicist Leonard Susskind, “It is part of a much bigger set of questions about how to think about probabilities in an infinite universe in which everything that can occur, does occur, infinitely many times.”

If you think it is odd that respected scientists are actually discussing the possibility of floating brains spontaneously forming, well this is just one of the strange predictions that current multiverse theories tend to create. When one proposes the existence of an infinite number of possible universes based on an infinite variety of laws and constants, then anything is possible in some universe somewhere.

So is there a universe somewhere in which the laws of matter and energy are fine-tuned to support the existence of Flying Spaghetti Monsters? This would seem to be the logical outcome of the most extreme multiverse theories. I have hesitated to bring this argument up until now, because I am not a theoretical physicist and I do not understand the mathematics behind multiverse theory. However, I recently came across an article by Marcelo Gleiser, a physicist at Dartmouth College, who sarcastically asks “Do Fairies Live in the Multiverse? Discussing multiverse theories, Gleiser writes:

This brings me to the possible existence of fairies in the multiverse. The multiverse, a popular concept in modern theoretical physics, is an extension of the usual idea of the universe to encompass many possible variations. Under this view, our universe, the sum total of what’s within our “cosmic horizon” of 46 billion light years, would be one among many others. In many theories, different universes could have radically different properties, for example, electrons and protons with different masses and charges, or no electrons at all.

As in Jorge Luis Borges’ Library of Babel, which collected all possible books, the multiverse represents all that could be real if we tweaked the alphabet of nature, combining it in as many combinations as possible.

If by fairies we mean little, fabulous entities capable of flight and of magical deeds that defy what we consider reasonable in this world, then, yes, by all means, there could be fairies somewhere in the multiverse.

So, here we have a respected physicist arguing that the logical implication of existing multiverse theories, in which every possibility exists somewhere, is that fairies may well exist. Of course, Gleiser is not actually arguing that fairies exist — he is pointing out what happens when certain scientific theories propose infinite possibilities without actually being testable.

But if multiverse theories are correct, maybe the Flying Spaghetti Monster does exist out there somewhere.